Program Evaluation Methods
Archived information
Archived information is provided for reference, research or recordkeeping purposes. It is not subject à to the Government of Canada Web Standards and has not been altered or updated since it was archived. Please contact us to request a format other than those available.
Chapter 5 - ANALYTICAL METHODS
5.1 Introduction
The analytical methods used in an evaluation should be set out clearly in the design phase. Data should never be collected unless the evaluator knows beforehand exactly how such data will be used in the analysis. A coherent evaluation design will consider three things: the issues, the analysis methods and the data that can be collected. All of the pieces must fit together before the evaluation proceeds.
This chapter describes the analytical methods the federal government uses to determine program results. It focuses on using these methods as an element in a particular evaluation strategy. Clearly, these methods may also be useful in other parts of the evaluation. For example, the evaluation assessment phase usually involves some exploratory analysis to help define the issues and to identify useful research methods. In addition, analysis pulls together the findings of the individual evaluation strategies used.
This chapter describes both the analysis of the direct measurement of program impacts and the analysis that uses measures of direct impacts to estimate a variety of indirect impacts. Direct analysis methods are divided into statistical and non-statistical methods. Several different types of indirect analysis methods are also described.
5.2 Statistical Analysis
Statistical analysis involves the manipulation of quantitative or qualitative (categorical) data to describe phenomena and to make inferences about relationships among variables. The data used can be "hard" objective data or "softer" subjective data. Both sorts of data must be described or organized in some systematic manner. Almost all analytical studies use statistical analysis. Using statistical analysis well, however, requires skill and an understanding of the assumptions that underlie the analysis.
Statistical analysis has two main purposes. The first is descriptive, involving statistical tabulations to present quantitative or qualitative data in a concise and revealing format. The second use of statistical models is for inference; that is, to test relationships among variables of interest and to generalize the findings to a larger population (based on the sample).
Reporting the findings of evaluation studies often involves the presentation of a lot of data in a concise manner. Statistical tabulations, graphical displays and statistics, such as the mean or the variance, can depict key characteristics of the data.
To demonstrate the use of descriptive statistical analysis, consider the case of a second-language educational program where immigrants have been tested before and after participation. Two examples of displays of the test scores in summary form (A and B) are shown in Table 3. Both involve descriptive summaries of the data; the second example (B) is more desegregated (less concise) than the first. In the first example (A), the mean score (arithmetic average) is presented. This statistic summarizes an average score without elaborating on the spread or distribution of scores. As is readily observable, the average score of the 43 people finishing the program was 64.7, compared to an average pre-program score of 61.2.
|
Table 3 - Examples of Descriptive Statistics |
|||||||||||||
|
(A) Displaying Average Scores |
|||||||||||||
|
Mean Scores |
Number Taking Test |
||||||||||||
| Pre-program Test |
61.2 |
48 |
|||||||||||
| Post-program Test |
64.7 |
43 |
|||||||||||
|
(B) Displaying the Distribution of Scores |
|||||||||||||
|
0-20 |
21-40 |
41-60 |
61-80 |
81-100 |
N |
||||||||
| Pre-program Test |
6 |
5 |
8 |
24 |
5 |
48 |
|||||||
|
Standard Deviation = 22.6 |
|||||||||||||
| Post-program Test |
5 |
5 |
6 |
20 |
7 |
43 |
|||||||
|
Standard Deviation = 23.7 |
|||||||||||||
The second example (B), on the other hand, displays the general distribution of scores, using the same raw data used in (A). For example, 6 of the pre-program people scored in the 0-20 per cent range and 20 of the post-program people scored in the 61-80 per cent range. The distribution of scores can also be displayed in percentage terms, as shown in brackets: 50 per cent (24 of 48) of the pre-program people scored in the 61-80 per cent range and 16.3 per cent (7 of 43) of the post-program people in the 81-100 per cent range. The percentage display also yields other, more aggregated descriptions of the data. For instance, 60.4 per cent of pre-program participants scored above 60 per cent on the test.
Finally, a statistic such as standard deviation can be used to summarize the spread of the distribution. The standard deviation indicates how closely the individual scores cluster around the arithmetic average (mean) score. The smaller the standard deviation in relation to the mean, the less the spread of the distribution.
Descriptive statistics need not be presented only in tabular form. Often data and statistics can be conveniently displayed in a visual format using graphs. Bar charts can be used to show distributions, and "pie" charts or boxes can be used to illustrate relative proportions. These visual displays can be easily generated by statistical software. A visual display can be a useful format for summarizing statistical information because it is often easier to read than a tabular format and readers do not necessarily need to understand all aspects of the statistics to obtain some information.
As indicated earlier, subjective (attitudinal) data can be treated the same way as more objective data. Suppose that individuals in the education program were asked to rate their improvement on a scale of 1-5. The results could be presented as follows.
|
1 |
2 |
3 |
4 |
5 |
Number |
|
| Number Responding |
16 |
38 |
80 |
40 |
26 |
200 |
| Percentage |
8% |
19% |
40% |
20% |
13% |
|
|
Average score 3.1 |
||||||
In this case, 40 of the 200 respondents (20 per cent) gave their improvement a rating of 4. The average improvement was 3.1. While the reliability and validity of this measuring technique might be questioned, the evaluator is able to summarize concisely the 200 attitudinal responses using simple descriptive statistical analysis.
The second major use of statistical analysis is for making inferences: to draw conclusions about the relationships among variables and to generalize these conclusions to other situations. In the example from Table 3, if we assume that the people taking the pre- and post-program tests are a sample of a larger population, then we must determine whether the apparent increase in test scores is a real increase owing to the program (or to other intervening factors), or only a difference arising from chance in the sampling (sampling error). Statistical methods, such as analysis of variance (ANOVA), can determine if the average scores are significantly different statistically.
Note that all that is being established in this case is a relationship, namely that the post-program score is higher than the pre-program score. To conclude that the program caused this result requires consideration of the threats to internal validity discussed in chapters 2 and 3. Statistical tests, such as analysis of variance, show only that there is indeed a statistically significant difference between the pre-program score and the post-program score. These tests do not demonstrate whether the difference can be attributed to the program. Other statistical tests and additional data can help answer attribution questions.
As another example of establishing relationships among variables through statistical analysis, consider the data in Table 4, which shows the pre-program and post-program test results (in percentage terms) for males and females. These descriptive statistics may reveal different effects of a program for different groups of participants. For example, the first part of Table 4 indicates little change between pre-program to post-program for male participants. Thus, the descriptions suggest the possibility that the program had different impacts on different recipients. These differences may offer important clues for further tests of statistical significance.
Looking at the data in tables 3 and 4, evaluators could use inferential statistical analysis to estimate the strength of the apparent relationship and, in this case, to show that the program had a greater impact on women than on men. Statistical methods such as regression analysis (or log-linear analysis) could establish the significance of the correlation among variables of interest. The relationship between scores, participation in the program and the sex of the participant could be determined. These kinds of statistical techniques could help establish the strength of the relationships between program outcomes and the characteristics of participants in the program.
Note that, while the statistical techniques referred to above (such as regression analysis) are often associated with inferential statistical analysis, many descriptive statistics are also generated as part of the process. The evaluator should distinguish between the arithmetical procedure of, say, estimating a regression coefficient, and the procedure of assessing its significance. The first is descriptive, the second inferential. This distinction is especially important to keep in mind when using statistical software to generate many descriptive statistics. The evaluator must draw appropriate inferences from the descriptive statistics.
|
Table 4 - Further Descriptive Data |
|||||
| Distribution of Scores By Sex | |||||
|
MALES |
|||||
|
0-20 |
21-40 |
41-60 |
61-80 |
81-100 |
|
| Pre-program Test |
13% |
15% |
38% |
20% |
14% |
| Post-program Test |
13% |
14% |
33% |
22% |
18% |
|
FEMALES |
|||||
| Pre-program Test |
10% |
16% |
32% |
32% |
10% |
| Post-program Test |
8% |
4% |
23% |
42% |
23% |
Statistical analysis can also be used to permit findings associated with one group to be generalized to a larger population. The pre- and post-program average scores shown in Table 3 may be representative of the larger total immigrant population, if appropriate sampling procedures were used and if suitable statistical methods were used to arrive at the estimates. If the group tested was large enough and statistically representative of the total immigrant population, one could expect that similar results would be achieved if the program were expanded. Properly done, statistical analysis can greatly enhance the external validity of any conclusions.
Statistical methods vary, depending on the level of measurements involved in the data (categorical, ordinal, interval and ratio) and on the number of variables involved. Parametric methods assume that the data are derived from a population with a normal (or another specific) distribution. Other "robust" methods permit significant departures from normality assumptions. Many non-parametric (distribution-free) methods are available for ordinal data.
Univariate methods are concerned with the statistical relationship of one variable to another, while multivariate methods involve the relationship of one (or more) variables to another set of two (or more) variables.
Multivariate methods can be used, for example, to discern patterns, make fair comparisons, sharpen comparisons and study the marginal impact of a variable (while holding constant the effects of other factors).
Multivariate methods can be divided into those based on the normal parametric general linear model and those based on the more recently developed methods of multivariate categorical data analysis, such as log-linear analysis. They may also be classified into two categories:
- methods for the analysis of dependence, such as regression (including analysis of variance or covariance), functional representation, path analysis, time series, multiple contingency, and similar qualitative (categorical) and mixed methods; and
- methods for the analysis of interdependence, such as cluster analysis, principal component analysis, canonical correlation and categorical analogues.
Strengths and Weaknesses
-
Statistical analysis can summarize the findings of an evaluation in a clear, precise and reliable way. It also offers a valid way of assessing the statistical confidence the evaluator has in drawing conclusions from the data.
While the benefits of statistical analysis are many, there are a number of caveats to consider.
-
Good statistical analysis requires expertise.
Evaluators should consult a professional statistician at both the design phase and at the analysis phase of an evaluation. One should not be seduced by the apparent ease of statistical manipulation using standard software.
-
Not all program results can be analyzed statistically.
For example, responses to an open-ended interview question on program results may provide lengthy descriptions of the benefits and the negative effects of the program, but it may be very difficult to categorize-let alone quantify-such responses neatly for statistical analysis without losing subtle but important differences among the responses.
-
The way data are categorized can distort as well as reveal important differences.
Even when an evaluator has quantitative information, he or she should take care in interpreting the results of statistical analyses. For instance, the data reflected in Table 3 could be presented differently, as shown in Table 5. Although the initial data are the same, the results in Table 5 seem to reveal a much stronger effect than those in Table 3. This indicates the importance of additional statistical methods, which can assess the strength of the apparent relationships. In other words, before concluding that the apparent differences in Table 3 or Table 5 are the results of the program, further inferential statistical analysis would be required.
|
Table 5 - Example of Descriptive Statistics |
||||
|
(A) Displaying Median Scores |
||||
| Pre-program Test | 58.4 | |||
| Post-program Test | 69.3 | |||
|
(B) Displaying the Distribution of Scores |
||||
|
0-35 |
36-70 |
71-100 |
N |
|
| Pre-program Test |
10 |
28 |
10 |
48 |
| Post-program Test |
6 |
11 |
26 |
43 |
-
Practitioners of statistical analysis must be aware of the assumptions as well as the limitations of the statistical technique employed.
A major difficulty with analytical methods is that their validity depends on initial assumptions about the data being used. Given the widespread availability of statistical software, there is a danger that techniques may depend on the data having certain characteristics that they do not in fact have. Such a scenario could, of course, lead to incorrect conclusions. Consequently, the practitioner must understand the limitations of the technique being used.
-
Multivariate statistical methods are especially susceptible to incorrect usage that may not, at first glance, be apparent. In particular, the technique depends on correctly specifying the underlying causal model.
-
Some possible pitfalls that exist when using multivariate regression include the following:
- explaining away a real difference;
- adding noise to a simple pattern;
- generating undue optimism about the strength of causal linkages made on the basis of the data; and
- using an inappropriate analytical approach.
References: Statistical Analysis
Behn, R.D. and J.W. Vaupel. Quick Analysis for Busy Division Makers. New York: Basic Books, 1982.
Casley, D.J. and K. Kumar. The Collection, Analysis and Use of Monitoring and Evaluation Data. Washington, D.C.: World Bank, 1989.
Fienberg, S. The Analysis of Cross-classified Categorical Data, 2nd edition. Cambridge, MA: MIT, 1980.
Hanley, J.A.. "Appropriate Uses of Multivariate Analysis," Annual Review of Public Health. Palo Alto, CA: Annual Reviews Inc., 1983, pp. 155-180.
Hanushek, E.A. and J.E. Jackson. Statistical Methods for Social Scientists. New York: Academic Press, 1977.
Hoaglin, D.C., et al. Data for Decisions. Cambridge, MA: Abt Books, 1982.
Morris, C.N. and J.E. Rolph. Introduction to Data Analysis and Statistical Inference. Englewood Cliffs, NJ: Prentice Hall, 1981.
Ragsdale, C.T. Spreadsheet Modelling and Decision Analysis. Cambridge, MA: Course Technology Inc., 1995.
5.3 Analysis of Qualitative Information
Non-statistical analysis is carried out, for the most part, on qualitative data-such as detailed descriptions (as in administrative files or field journals), direct quotations in response to open-ended questions, the transcripts of group discussions and observations of different types. This topic was discussed briefly in section s 4.1 and 4.4 through 4.7. The following section provides only a brief discussion of non-statistical analysis. For a more detailed description, consult the references cited at the end of this section .
The analysis of qualitative data-typically in conjunction with the statistical (and other types of) analysis of quantitative data-can provide a holistic view of the phenomena of interest in an evaluation. The process of gathering and analyzing qualitative information is often inductive and "naturalistic": at the beginning of data collection or analysis, the evaluator has no particular guiding theory concerning the phenomena being studied. (Another type of non-statistical analysis of quantitative data is discussed in section 5.5, which covers the use of models.)
Non-statistical data analysis may rely on the evaluator's professional judgement to a greater degree than is the case with other methods, such as statistical analysis. Consequently, in addition to being knowledgeable about the evaluation issues, evaluators carrying out non-statistical analysis must be aware of the many potential biases that could affect the findings.
Several types of non-statistical analysis exist, including content analysis, analysis of case studies, inductive analysis (including the generation of typologies) and logical analysis. All methods are intended to produce patterns, themes, tendencies, trends and "motifs," which are generated by the data. They are also intended to produce interpretations and explanations of these patterns. The data analysis should assess the reliability and validity of findings (possibly through a discussion of competing hypotheses). The analysis should also analyze "deviant" or "outlying" cases. It should "triangulate" several data sources, and include collection or analytical methods.
The four main decisions to be made in non-statistical data analysis concern the analytical approach to be used (such as qualitative summary, qualitative comparison, or descriptive or multivariate statistics); the level of analysis; the time at which to analyze (which includes decisions about recording and coding data and about quantifying this data); and the method used to integrate the non-statistical analysis with related statistical analysis.
Although non-statistical (and statistical) data analysis typically occurs after all the data have been collected, it may be carried out during data collection. The latter procedure may allow the evaluator to develop new hypotheses, which can be tested during the later stages of data collection. It also permits the evaluator to identify and correct data collection problems and to find information missing from early data collection efforts. On the other hand, conclusions based on early analysis may bias later data collection or may induce a premature change in program design or delivery, making interpretation of findings based on the full range of data problematic.
Non-statistical data analysis is best done in conjunction with the statistical analysis of related (quantitative or qualitative) data. The evaluation should be designed so that the two sorts of analysis, using different but related data, are mutually reinforcing or at least illuminating.
Strengths and Weaknesses
-
The major advantages of non-statistical data analysis are that many hard-to-quantify issues and concepts can be addressed, providing a more holistic point of view
In addition, non-statistical analysis allows the evaluator to take advantage of all the available information. The findings of a non-statistical analysis may be more richly detailed than those from a purely statistical analysis.
-
However, conclusions based solely on non-statistical analysis may not be as accurate as conclusions based on multiple lines of evidence and analysis.
-
The validity and accuracy of the conclusions of non-statistical analysis depend on the skill and judgement of the evaluator, and its credibility depends on the logic of the arguments presented.
Cook and Reichardt (1979), Kidder and Fine (1987), and Pearsol (1987), among others, discuss these issues in greater detail.
References: Non-statistical Analysis of Qualitative Information
Cook, T.D. and C.S. Reichardt. Qualitative and Quantitative Methods Evaluation Research. Thousand Oaks: Sage Publications, 1979.
Guba, E.G. "Naturalistic Evaluation," in Cordray, D.S., et al., eds. Evaluation Practice in Review. V. 34 of New Directions for Program Evaluation. San Francisco: Jossey-Bass, 1987.
Guba, E.G. and Y.S. Lincoln. Effective Evaluation: Improving the Usefulness of Evaluation Results Through Responsive and Naturalistic Approaches. San Francisco: Jossey-Bass, 1981.
Krueger, R.A. Focus Groups: A Practical Guide for Applied Research. Thousand Oaks: Sage Publications, 1988.
Levine, M. "Investigative Reporting as a Research Method: An Analysis of Bernstein and Woodward's All the President's Men," American Psychologist. V. 35, 1980, pp. 626-638.
Miles, M.B. and A.M. Huberman. Qualitative Data Analysis: A Sourcebook of New Methods. Thousand Oaks: Sage Publications, 1984.
Nachmias, C. and D. Nachmias. Research Methods in the Social Sciences. New York: St. Martin's Press, 1981, Chapter 7.
Patton, M.Q. Qualitative Evaluation Methods. Thousand Oaks: Sage Publications, 1980.
Pearsol, J.A., ed. "Justifying Conclusions in Naturalistic Evaluations," Evaluation and Program Planning. V. 10, N. 4, 1987, pp. 307-358.
Rossi, P.H. and H.E. Freeman. Evaluation: A Systematic Approach, 2nd edition. Thousand Oaks: Sage Publications, 1989.
Van Maasen, J., ed. Qualitative Methodology. Thousand Oaks: Sage Publications, 1983.
Webb, E.J., et al. Nonreactive Measures in the Social Sciences, 2nd edition. Boston: Houghton Mifflin, 1981.
Williams, D.D., ed. Naturalistic Evaluation. V. 30 of New Directions for Program Evaluation. San Francisco: Jossey-Bass, 1987.
5.4 Analysis of Further Program Results
Evaluations typically attempt to measure the direct results of programs. But there frequently are longer-term or broader program impacts that are also of interest. One may frequently analyze further program results by analytically tracing the measured direct results to further impacts. In Chapter 1, three levels of program results were distinguished:
- outputs (which are often operational in nature);
- intermediate outcomes (including benefits to program clients and, sometimes, unintended negative effects on clients and others); and
- final outcomes (which are closely linked to the program's objectives and usually to the broad benefits sought by the government, i.e., economic benefits or health, safety and welfare objectives).
The general format for such analysis uses an established analytical model to trace results of the first and second type to results of the third type (or to different results of the second type).
| Program Activities |
» | Operational Outputs/ Client Benefits |
» | Client Benefits/ Broader Outcomes |
The use of this analysis method can be demonstrated simply. Consider the program that teaches reading skills to immigrants, where these skills are presumed to result in better job opportunities. This program logic is shown pictorially as follows.
| Reading Program |
» | Increased Reading Skills |
» | Higher Income/ Better Employment Prospects |
An evaluation strategy to assess the incremental impact of the reading program on reading skills would be developed and measurements would be taken. An established model would then be used to transform the observed reading skill changes into projected job-related and income impacts: the increases in reading skills observed would be translated into job and income effects, based on prior research that relates these variables to reading skills.
Note that any such analysis is an alternative to direct assessment of the broader results of a program. In the above example, the evaluator could measure directly the effect of the program on participants' ability to obtain higher-income jobs. For example, the evaluator might use a quasi-experimental design to compare a program group with a control group, and determine if the treatment group had increased their job income relative to the control group. There are, however, a number of reasons why more indirect methods may be preferable.
-
The analysis of broader results allows for the timely estimation of impacts that occur over the long term.
Often the derived impacts are longer term, and the exigencies of an evaluation might not allow for follow-up over long periods.
-
Analyzing broader results allows the evaluator to assess impacts that are difficult to measure directly.
It may be extremely difficult or complex to assess broader results directly, particularly in the course of a specific evaluation project. In a sense, these methods reduce the risk of the evaluation study. By measuring the more immediate results first, one can be confident that at least some results are validly measured. By going straight to the broader results, which may be difficult to measure, one may end up with no valid results measures at all.
-
Analyzing broader results is useful for assessing broader impacts that have already been researched.
Because of the measurement difficulties described above, the evaluator might wish to use a relationship between the shorter term and broader impacts of a program established through previous research (depending, of course, on whether such research is available). For instance, in the reading program example above, it is likely that extensive research has been carried out to investigate the relationship between reading skills, job opportunities and income. Here the evaluator could rely on this research to focus the evaluation strategy on measuring the improvements in reading skills produced by the program; the higher incomes that likely follow will already have been established by previous research.
5.5 The Use of Models
Every evaluation that asserts that certain results flow from program activities is based on a model, whether implicit or explicit. With no underlying theory of how the program causes the observed results, the evaluator would be working in the dark and would not be able to credibly attribute these results to the program. This is not to say that the model must be fully formed at the start of the evaluation effort. Generally, it will be revised and refined as the evaluation team's knowledge grows.
The various disciplines within the social sciences take somewhat different approaches to their use of models, although they share many common characteristics.
The models discussed in this section are
- simulation models;
- input-output models;
- micro-economic models;
- macro-economic models; and
- statistical models.
5.5.1 Simulation Models
Simulation can be a useful tool for evaluators. Any transformation of program inputs into outputs that can be set out in a spreadsheet can be modelled by evaluators with some training and practice.
An explicit quantitative model may be set out because the data are uncertain. When one is dealing with ranges rather than single numbers, and wrestling with probabilities, being able to simulate likely outputs or outcomes can be an essential skill. In the 1990s, software that adds simulation capabilities to ordinary spreadsheets has brought this skill within reach of many evaluators who might have used less quantitative approaches before.
A simulation model can transform input data into results data. For example, consider a customs program at highway border points. Suppose a new set of questions is used at the entry point. If this new set of questions takes, on average, 11 seconds longer to administer than the previous set of questions, a model could be used to assess its effect on the average waiting time of clients.
A simulation has three main components: input data, a mathematical model and output data. Simulations use two main types of mathematical models: stochastic models, which incorporate a random data generator, and deterministic models, which do not.
In some ways, simulation resembles other statistical techniques, such as regression analysis. In fact, these techniques may be used to build the model. Once the model is constructed, however, it treats its inputs as data to be acted on by the model, rather than as information on which to base the model. The mathematical model generates output data that can be checked against actual outcomes in the real world.
Evaluators are increasingly interested in one type of simulation model, a risk model based on a cost-benefit spreadsheet. When the inputs to the cost-benefit model are given as ranges and probabilities (rather than as single certain figures), a risk model produces range and probability information about the bottom line (normally the net present value). This information on range and probability can be very useful to a manager seeking to assess the risk of a program, or to an evaluator estimating materiality and risk. (See Section 5.6, Cost-benefit and Cost-effectiveness Analysis.)
Strengths and Weaknesses
The main strength of simulation is that it allows the evaluator to estimate incremental effects in complex and uncertain situations. The main limitation of the technique is that it requires a sophisticated understanding of the dynamics of the program, as well as some skill in building quantitative models.
It should be noted, as well, that simulation models can provide valuable ex ante information; that is information on the probable impacts of a given course of action before this course of action is embarked upon. Clearly information of this sort can be very useful in ruling out undesirable alternatives. Ex post, the actual impact of a new program or changes to an existing program is best estimated through empirical methods such as regression analysis or the designs discussed in Chapter 3.
References: Simulation
Buffa, E.S. and J.S. Dyer. Management Science Operations Research: Model Formulation and Solution Methods. New York: John Wiley and Sons, 1977.
Clemen, R.T. Making Hard Decisions. Duxbury Press, 1991, section s 1-3.
Ragsdale, C.T. Spreadsheet Modelling and Decision Analysis. Cambridge, MA: Course Technology Inc., 1995.
5.5.2 Input-output Models
An input-output model is a static economic model designed to depict the mutual interdependence among the different parts of an economy. The model describes the economy as a system of interdependent activities-activities that act on one another directly and indirectly. An input-output model describes how one industry uses the outputs of other industries as inputs, and how its own outputs are used by other companies as inputs. An input-output model is a systematic deconstruction of the economy describing the flow of goods and services necessary to produce finished products (goods and services).
An input-output model can be used to derive internally consistent multisector projections of economic trends and detailed quantitative assessments of both the direct and indirect secondary effects of any single program or combination of programs. Specifically, an input-output model can produce a detailed description of the way a government program affects the production and consumption of goods and services today.
The input structure of each producing sector is explained in terms of its technology. "Technical coefficients" outline the amount of goods and services, including labour, required by a sector to produce one unit of output. The model specifies technical coefficients. The model also specifies a set of "capital coefficients", which describes the stocks of buildings, equipment and inventories required to transform the proper combination of inputs into outputs. Consumption patterns outline the demand for inputs (such as income) by all producing sectors of the economy, including households. These patterns can be analyzed along with the production and consumption of any other good or service.
The usefulness of an input-output model can be demonstrated by considering the impact of hypothetical selective taxation measures on employment in the telecommunications sector. Suppose the tax measures provide preferential treatment to the sector and therefore directly influence the level, composition and price of sector outputs. This, in turn, influences the demand for and use of labour in the sector. The model consists of coefficients outlining the present state-of-the-art technology and of equations outlining the expected consumption and production of each sector.
First, changes resulting from the selective tax measures can be estimated using the expected consumption and production of telecommunication equipment. Then, the input-output model can take as its input the increase in telecommunications equipment consumption. The model will yield as output the estimated increase in telecommunications labour flowing from the tax measures.
Strengths and Weaknesses
Historically, input-output models were used much more frequently by centrally planned economies. Input-output models tend to be static one-period models, which are essentially descriptive, and therefore are not very effective for inferring probable policy effects in the future.
Unfortunately, input-output models have been frequently misused in evaluations. In particular, program expenditures in one sector have been run through the model to estimate supposed "impacts" without taking into account the offsetting negative effects generated by the taxes or borrowing necessary to support the program.
Another limitation in a changing economy is that input-output models may not include changes in the production coefficients that result from technological developments or from relative price changes among inputs. Thus, when these changes occur, the input-output model would describe an incorrect input composition for an industry. This in turn would result in incorrect estimates of additional program results. The Statistics Canada input-output model is inevitably based on information that is some years out of date. In addition, being a macro model, it is not especially well adapted to depicting the effects of small expenditures typical of most programs.
References: Input-output Models
Chenery, H. and P. Clark. Inter-industry Economics. New York: John Wiley and Sons, 1959.
Leontief, W. Input-output Economics. New York: Oxford University Press, 1966.
Statistics Canada. The Input-output Structures of the Canadian Economy 1961-81. Ottawa: April 1989, Catalogue 15-201E.
5.5.3 Micro-economic Analysis
A micro-economic model describes the economic behaviour of individual economic units (people, households, firms or other organizations) operating within a specific market structure and set of circumstances. Since most programs are directed exactly at this level, such models can be quite useful to evaluators. The price system is the basis of micro-economic models. Micro-economic models are typically represented by equations depicting the demand and supply functions for a good or service. These equations describe the relationship between price and output and can frequently be represented graphically by demand and supply curves.
A number of assumptions constrain the manner in which micro-economic models perform. For example, consumers are assumed to maximize their satisfaction, and to do so rationally. Bearing in mind the assumptions that underlie micro-economic models, these models can be used to predict market behaviour, optimal resource input combinations, cost function behaviour and optimal production levels.
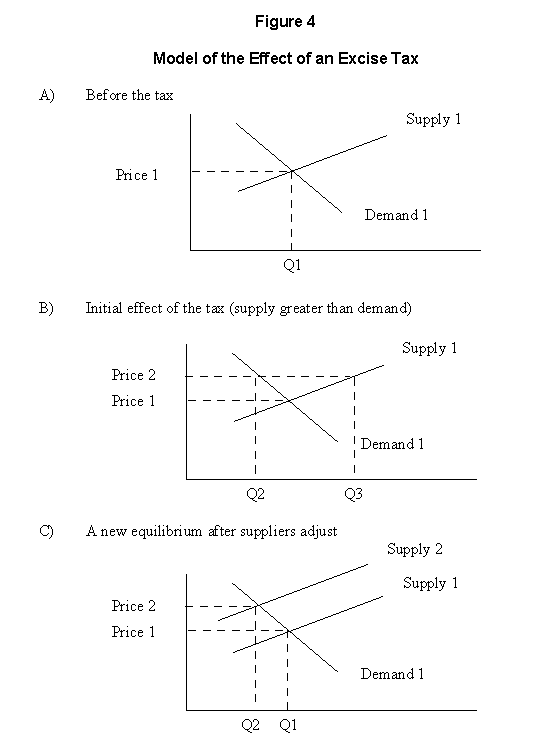
Micro-economic models can be used to estimate program results insofar as prices and outputs can describe program impacts. Figure 4 is an example of how a micro-economic model could describe the effect of a cigarette excise tax program on the income of cigarette manufacturers or on smoking by teenagers.
According to Figure 4, the price and quantity of cigarettes produced and consumed before the excise tax were P0 and Q0, respectively. The excise tax increased the cost of cigarettes; this is represented by an upward shifting supply curve in the micro-economic model. As a result, the new price is higher and the new output level is lower than it was before the introduction of the excise tax. Before the tax, the cigarette industry received P0 x Q0 revenue; after the tax, the cigarette industry received P1 x Q1 revenue. The reduction in revenue to the cigarette industry as a result of the excise tax will depend on the slopes of the demand and supply curves, which themselves are determined by several factors.
Strengths and Weaknesses
Building a micro-economic model of program effects normally requires an economist. Such models are often worthwhile, since they can be highly informative about the rationale for a program and can provide a basis for measuring impacts and effectiveness.
References: Microeconomic Analysis
Henderson, J. and R. Quandt. Micro-economic Theory. New York: McGraw-Hill, 1961.
Polkinghorn, R.S.. Micro-theory and Economic Choices. Richard Irwin Inc., 1979.
Samuelson, P. Foundations of Economic Analysis. Cambridge, MA: Harvard University Press, 1947.
Watson, D.S. Price Theory in Action. Boston: Houghton Mifflin, 1970.
5.5.4 Macro-economic Models
Macro-economic models deal mainly with inflation, unemployment and large aggregates such as the gross national product. Various macro-economic models attempt to explain and predict the relationships among these variables.
The utility of a macro-economic model is that it suggests what economic impacts-such as increased output, income, employment, interest rates or inflation-are most likely to occur when a given monetary and fiscal policy (or program) is put into place.
As an example of a macro-economic model, suppose an evaluator wanted to assess the impact on employment of a government program that subsidizes certain types of exports. Suppose further that the effect of the program on export sales had already been measured. Incremental export sales figures would then be fed into a macro-economic model of the Canadian economy and the model could estimate the effect on employment.
Strengths and Weaknesses
The advantage of using a macro-economic model is that the model identifies critical links between aggregate broad variables. Also, this kind of model provides an overall picture, which can be used to compare Canadian programs to similar programs in other countries (provided assumptions and model validity criteria remain intact).
However, there are serious limitations to the applicability of macro-economic models to program evaluation. Macro-economic models may yield erroneous results if they omit key factors. Furthermore, input data are usually derived from another model rather than directly measured, adding an extra layer of uncertainty.
Many macro-economic models have poor predictive capability, especially in the short run. They can be appropriately used, however, if the derived impacts are long term, and if the program is large relative to the economy.
References: Macro-economic Analysis
Gordon, R.A. Economic Instability and Growth: The American Record. Harper & Row, 1974.
Heilbroner, R.L. and L.C. Thurow. Economics Explained. Toronto: Simon and Schuster Inc., 1987.
Nelson, R., P. Merton and E. Kalachek. Technology, Economic Growth and Public Policy. Washington, D.C.: Brookings Institute, 1967.
Okun, A. The Political Economy of Prosperity. Norton, 1970.
Silk, L. The Economists. New York: Avon Books, 1976.
5.5.5 Statistical Models
Many types of statistical models are used in evaluation studies. The most simple model is a tabulation of data for a single variable, organized to make the shape of the data visible. Cross-tabulations of two variables are a basic tool of evaluation analysis and reporting. Even data analyzed using other models are often reported in cross-tabulations, because these tabulations are more transparent and accessible to decision makers than more sophisticated models.
Typically, clinical programs (health and education, for example) face small sample constraints and will therefore rely on "analysis of variance" models to identify the effects of the program. Larger programs (trade subsidies or employment programs, for example) normally produce large data sets and can therefore rely on regression-based "linear models" to identify effects. Most federal government programs are of the latter type, so this section will concentrate on them.
Regression analysis can be used to test a hypothesized relationship, to identify relationships among variables that might explain program outcomes, to identify unusual cases (outliers) that deviate from the norms, or to make predictions about program effects in the future. The technique is sometimes exploratory (back-of-the-envelope line-fitting), but more often it is used as the final confirmation and measurement of a causal relationship between the program and observed effects. In fact, it is important that the regression model be based on a priori reasoning about causality. Data fishing expeditions, which produce "garbage-in garbage-out" results, should be avoided. One way to avoid this is to specify and calibrate the model using only half the data available and then see whether the model is a good predictor of outcomes shown in the other half of the data. If this is the case, then the model is probably robust.
Remember that correlation does not necessarily imply causality. For example, two variables may be correlated only because they are both caused by a third. High daily temperatures and the number of farm loans may be correlated because they both tend to occur in the summer; but this does not mean that farm loans are caused by the temperature.
Another common problem with regression models is to mistake the direction of causality. One might observe, for example, that businesses sell more overseas after they get incentive grants from a government trade program. However, it may well be that the companies that sell more overseas are more credible and therefore enjoy more success in getting grants; it may be the overseas sales that cause the grants rather than the reverse.
Statistical models are often vital in identifying incremental effects. For example, Health Canada might use an epidemiological model to identify the effects of its National AIDS Strategy. The Department of Finance Canada would use an incomes model to estimate the tax effects of a proposed family welfare benefit. To be able to build such models generally takes in-depth expertise in the program area, as well as expertise in the statistical technique used.
Strengths and Weaknesses
Statistical models are versatile and, if properly constructed, will provide very useful estimates of program results. On the other hand, statistical models must be appropriately specified and validated to provide reliable results, which is not always as straightforward a task as it may at first appear.
One weakness of statistical models is that the evaluator may not be able to draw inferences from them. For example, if the model covers only certain age groups or individuals in certain geographic areas, the evaluator may not be able to infer from his or her results the program's probable effects in other geographic areas or on other age groups.
References: Statistical Models
Chatterjee, S. and B. Price. Regression Analysis by Example, 2nd edition. New York: John Wiley and Sons, 1995.
Fox, J. Linear Statistical Models and Related Methods, with Applications to Social Research. New York: John Wiley and Sons, 1984.
Huff, D. How to Lie with Statistics. Penguin, 1973.
Jolliffe, R.F. Common Sense Statistics for Economists and Others. Routledge and Kegan Paul, 1974.
Mueller, J.H. Statistical Reasoning in Sociology. Boston: Houghton Mifflin, 1977.
Sprent, P. Statistics in Action. Penguin, 1977.
5.6 Cost-benefit and Cost-effectiveness Analysis
All programs aim to produce benefits that outweigh their costs. Having estimated the various costs and benefits derived from the program, evaluators can compare the two to determine the worthiness of the program. Cost-benefit and cost-effectiveness analysis are the most common methods used to accomplish this. Typically, these analyses provide information about the net present value (NPV) of a program. In the case of cost-benefit analysis, program benefits are transformed into monetary terms and compared to program costs. In cost-effectiveness analysis, program results in some non-monetary unit, such as lives saved, are compared with program costs in dollars.
At the planning stage, cost-benefit and cost-effectiveness assessments may be undertaken ex ante, "before the fact," based on estimates of anticipated cost and benefits. Most of the literature on cost-benefit analysis discusses it as a tool for ex ante analysis, particularly as a way to examine the net benefits of a proposed project or program involving large capital investments (see, for example, Mishan, 1972; Harberger, 1973; Layard, 1972; Sassone and Schaffer, 1978; and Schmid, 1989).
After a program has been in operation for some time, cost-benefit and cost-effectiveness techniques may be used ex post, "after the fact," to assess whether the actual costs of the program were justified by the actual benefits. For a more complete discussion of the use of cost-benefit analysis in evaluation, see Thompson (1980) or Rossi and Freeman (1989). Alternatively, an overview of cost-benefit analysis can be found in Treasury Board's Benefit-cost Analysis Guide (1997) and in the associated case studies.
Cost-benefit analysis compares the benefits of a program, both tangible and intangible, with its costs, both direct and indirect. After they are identified and measured (or estimated), the benefits and costs are transformed into a common measure, which is usually monetary. Benefits and costs are then compared by calculating a net present value. Where costs and benefits are spread over time, they must be discounted to some common year by using an appropriate discount rate.
To carry out a cost-benefit analysis, one must first decide on a point of view from which program's costs and benefits will be counted; this is usually the individual's perspective, the federal government's fiscal perspective or the social (Canada-wide) perspective. What are considered the costs and benefits of a program will usually differ from one perspective to the next. The most common perspective for cost-benefit analysis at the federal level is the social perspective, which accounts for all costs and benefits to society. However, the individual and government fiscal perspectives may help shed light on differing viewpoints about the worth of the program, or explain a program's success or failure. The differences between these three perspectives are discussed in greater detail in Rossi and Freeman (1989).
The individual perspective examines the program costs and the benefits to the program participant (which might be a person, a family, a company or a non-profit organization). Cost-benefit analyses done from such a perspective often produce high benefit-cost ratios because the government or society subsidizes the program from which the participant benefits.
The analysis from a federal government fiscal perspective values costs and benefits from the point of view of the funding source. It is basically a financial analysis, examining the financial costs and the direct financial benefits to the government. Typical cash flows that would be examined in such an analysis would include program administrative costs, direct cash outlays (grants), taxes paid to government (including corporate income taxes, personal income taxes, federal sales taxes and duties), reduced payments of unemployment insurance, and possible changes in equalization and transfer payments.
A social cost-benefit analysis, on the other hand, takes the perspective of society as a whole. This makes the analysis more comprehensive and difficult since the broader results of a program must be considered, and since market prices, which are a good measure of costs and benefits to an individual or an organization (government), might not accurately reflect the true value to society. They might be distorted by subsidies or by taxes, for example. The components of social cost-benefit analysis, although similar to those used in the individual and government analyses, are valued and priced differently (see Weisbrod, et al., 1980). For example, society's opportunity costs are different from the opportunity costs incurred by a participant in a program. Another difference would involve the treatment of transfer payments: transfer payments should be excluded from costs in a social cost-benefit analysis since they would also have to be entered as benefits to society, hence cancelling themselves out.
Cost-benefit analyses using the government or social perspectives tend to produce lower benefit-cost ratios than those using the individual perspective. This is because government or society generally bears the entire cost of the program (as opposed to individuals, who may receive all the benefits but bear only a small fraction of the program's total cost). Nevertheless, the social perspective should be used for a cost-benefit analysis of a government program.
Cost-effectiveness analysis also requires the quantification of program costs and benefits, although the benefits (or effects) will not be valued in dollars. The impact or effectiveness data must be combined with cost data to create a cost-effectiveness comparison. For example, the results of an educational program could be expressed, in cost-effectiveness terms, as "each $1,000 of program dollars (cost data) results in an average increase of one reading grade (results data)". In cost-effectiveness analysis, benefits (or effects) are expressed on some quantitative scale other than dollars.
Cost-effectiveness analysis is based on the same principles as cost-benefit analysis. The assumptions, for example, in costing and discounting are the same for both procedures. Cost-effectiveness analysis can compare and rank programs in terms of their costs for reaching given goals. The effectiveness data can be combined with cost data to determine the maximum effectiveness at a given level of cost or the least cost needed to achieve a particular level of effectiveness.
The data required for cost-benefit and cost-effectiveness studies can come from various sources. Clearly, searches of comprehensive program files should yield a significant amount of cost information. This can often be reinforced through surveys of beneficiaries. Benefit data would come from any or all of the other approaches discussed earlier in this publication.
For example, suppose an evaluation study was designed to test the hypothesis that a mental health program that strongly de-emphasized hospitalization in favour of community health care was more effective than the prevailing treatment method. Suppose further that an experimental design provided the framework for estimating the incremental effects of the alternative program. Once these incremental effects were known, cost-benefit analysis could be used to value the benefits and to compare them to the costs.
Strengths and Weaknesses
The strengths and weaknesses of cost-benefit and cost-effectiveness analysis are well documented (see, for example, Greer and Greer, 1982; and Nobel, 1977). Here, a number of brief points can be made about the strengths and weaknesses of cost-benefit analysis.
-
Cost-benefit analysis looks at a program's net worth.
Such analysis does not estimate specific benefits and costs, per se, but does summarize these benefits and costs so that one can judge and compare program alternatives. The extent to which objectives have been met will have to be measured elsewhere using another evaluation design and data collection methods. The results on program outcomes could then serve as input to the overall cost-benefit and cost-effectiveness analysis.
-
An evaluator must address the issue of attribution or incremental effect before doing a cost-benefit analysis.
For example, from 1994 to 1997, the federal government implemented an infrastructure program that shared costs with municipalities and provincial governments. Before one could analyze the costs and benefits of the program, or of alternative program designs, one would have to develop measures of incremental effect that would show to what extent the program changed or accelerated municipal infrastructure works. Only after incremental effects are known is it sensible to value and compare costs and benefits.
-
Cost-benefit and cost-effectiveness analyses often help evaluators identify the full range of costs and results associated with a program.
-
Cost-benefit and cost-effectiveness analyses, in themselves, do not explain particular outcomes and results.
These techniques do not determine why a specific objective was not met or why a particular effect occurred. However, by systematically comparing benefits and costs, these analyses are a key step toward providing accurate and useful advice to decision makers.
-
Many methodological problems are associated with these analyses.
The benefits and costs of a program often cannot be easily expressed in dollars. It can be very difficult to place dollar values on educational results, health results (the value of human life or its quality), or equity and income distribution results. Such valuations are and will remain highly debatable. Also, costs and benefits have to be discounted to a common point in time in order to be compared. The literature on cost-benefit analysis is far from unanimous on which discount rate to use. The Treasury Board Benefit-cost Guide recommends using a risk analysis (simulation) approach, with a range of rates centred on 10 per cent per annum, after inflation.
-
The evaluator should always conduct a sensitivity analysis of the assumptions underlying the cost-benefit and cost-effectiveness analyses to determine the robustness of his or her results.
Because of the assumptions that must be made to compare the benefits and costs of a program, a sensitivity analysis should be done to test the extent to which conclusions depend on each specific assumption. Further, the analysis should test the extent to which the conclusions will vary when these assumptions change. When the outcome of the analysis is highly dependent on a particular input value, then it may be worth the additional cost necessary to render more certain the value of that input. It should be emphasized that, unlike some other types of evaluation analysis, cost-benefit analysis allows the evaluator to conduct a rigorous and systematic sensitivity analysis.
-
Cost-effectiveness analysis is sometimes used when it is too difficult to convert to monetary values associated with cost-benefit analysis.
Cost-effectiveness analysis sometimes allows one to compare and rank program alternatives. However, since the benefits are not converted to dollars, it is impossible to determine the net worth of a program, or to compare different programs using the same criteria.
Cost-benefit analysis offers techniques whereby even costs and benefits that are difficult to measure in monetary terms can be compared and evaluated. However, this type of analysis often requires sophisticated adjustments to the measures of costs and benefits because of uncertain assumptions. This can make managers uneasy; they often suspect, sometimes with just cause, that such assumptions and adjustments are fertile ground for the manipulation of results in favour of any bias the analyst may have.
Furthermore, cost and benefit identification is often rendered more difficult by government departments and agencies that do not keep records that permit easy comparison. The cost records departments keep for most programs cut across many activities and are organized for the convenience of administrators, not evaluators.
References: Cost-benefit Analysis
Angelsen, Arild and Ussif Rashid Sumaila. Hard Methods for Soft Policies: Environmental and Social Cost-benefit Analysis. Bergen, Norway: Michelsen Institute, 1995.
Australian Department of Finance. Handbook of Cost-benefit Analysis. Canberra: 1991.
Belli, P. Guide to Economic Appraisal of Development Projects. Washington, D.C.: World Bank, 1996.
Bentkover, J.D., V.T. Covdlo and J. Mumpower. Benefits Assessment: The State of the Art. Dordrecht, Holland: D. Reidel Publishing Co., 1986.
Harberger, A.C. Project Evaluation: Collected Papers. Chicago: Markham Publishing Co., 1973.
Miller, J.C. III and B. Yandle. Benefit-cost Analyses of Social Regulation. Washington: American Enterprise Institute, 1979.
Office of the Auditor General of Canada. "Choosing and Applying the Right Evidence-gathering Techniques in Value-for-money Audits," Benefit-cost Analysis. Ottawa:1994, Appendix 5.Sang, H.K. Project Evaluation. New York: Wilson Press, 1988.
Sassone, P.G. and W.A. Schaffer. Cost-benefit Analysis: A Handbook. New York: Academic Press, 1978.
Schmid A.A. Benefit-cost Analysis: A Political Economy Approach. Boulder: Westview Press, 1989.
Self, P. Econocrats and the Policy Process: The Politics and Philosophy of Cost-benefit Analysis. London: Macmillan, 1975.
Skaburskis, Andrejs and Fredrick C. Collignon. "Cost-effectiveness Analysis of Vocational Rehabilitation Services," Canadian Journal of Program Evaluation. V. 6, N. 2, October-November 1991, pp. 1-24.
Skelton, Ian. "Sensitivity Analysis in Multi-criteria Decision Aids: A Demonstration of Child Care Need Assessment," Canadian Journal of Program Evaluation. V. 8, N. 1, April-May 1993, pp. 103-116.
Sugden, R. and A. Williams. The Principles of Practical Cost-benefit Analysis. Oxford: Oxford University Press, 1978.
Thompson, M. Benefit-cost Analysis for Program Evaluation. Thousand Oaks: Sage Publications, 1980.
Treasury Board of Canada, Secretariat. Benefit-cost Analysis Guide. Ottawa: 1997 (available in summer of 1997).
Van Pelt, M. and R. Timmer. Cost-benefit Analysis for Non-Economists. Netherlands Economic Institute, 1992.
Watson, Kenneth, "The Social Discount Rate," Canadian Journal of Program Evaluation, V. 7, N. 1, April-May 1992, pp. 99-118.
World Bank, Economic Development Institute. The Economics of Project Analysis: A Practitioner's Guide. Washington, D.C.: 1991.
Yates, Brian T. Analyzing Costs, Procedures, Processes, and Outcomes in Human Services. Thousand Oaks: Sage Publications, 1996.
5.7 Summary
Chapter 5 has outlined several methods of data analysis that should, in practice, form an integral part of an evaluation strategy. The parts of an evaluation strategy should constitute a coherent whole: evaluation issues, design, data collection methods and suitable data analysis should all fit together as neatly as possible.
This publication has discussed a wide variety of analytical methods: several types of statistical and non-statistical analysis for assessing program results, methods for estimating broader program impacts (including the use of models) and methods for assessing costs. Of course, it will remain difficult to decide when and how to skilfully and sensitively use particular methods.
- Date modified: